Содержание
Криптографические xэш - функции
- Хэширование
- преобразование исходного информационного массива произвольной длины в битовую строку фиксированной длины.
- Криптографическая хэш-функция
- хэш-функция, являющаяся криптографически стойкой, то есть удовлетворяющая ряду требований, специфичных для криптографических приложений.
Требования к криптографически стойким хэш-функциям :
- Для заданного значения хэш-функции
должно быть невозможно вычислить блок данных 
, для которого 
. - Стойкость к коллизиям первого рода: для заданного сообщения должно быть вычислительно невозможно подобрать другое сообщение
, для которого 
. - Стойкость к коллизиям второго рода: должно быть вычислительно невозможно подобрать пару сообщений
, имеющих одинаковый хэш.
Математически хэш функцию можно записать в виде:
,
где – исходное сообщение, – значение хеш-функции.
Для криптографических хэш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект).
Итеративная последовательная схема
Схема Меркеля-Дамгарда сегодня - основание для многих функций криптографического хэширования.
Для построения хэш-функций используется cтруктура Меркля-Дамгарда. Cжимающая функция 
преобразует 
блоков,размер каждого состоит из 
бит.
В качестве начального значения переменной 
используется произвольное вектор инициализации 
. Каждый следующий блок данных объединяется с выходным значением сжимающей функции на предыдущей итерации.
Если длина блока 
< , 
дополняется длиной сообщения и 
. Значением хэш-функции являются выходные бит последней итерации.
Функция сжатия
- Односторонняя функция сжатия
- функция для преобразования двух входных блоков фиксированной длины в выходной блок фиксированной длины.
В настоящее время популярны два подхода для создания хэш-функций. В первом подходе функция сжатия сделана на "пустом месте": она разработана только для этой цели. Во втором подходе блочный шифр с симметричными ключами служит функцией сжатия.
Хэш-функции, сделанные на "пустом месте"
MD5
Серия алгоритмов по построению дайджеста сообщения, была разработанна профессором Рональдом Л. Ривестом из Массачусетского технологического института. MD5 был выпущен в 1991 году для замены предыдущего алгоритма, MD4. Позже Гансом Доббертином(Hans Dobbertin) были найдены недостатки алгоритма MD4.В 1996 году Ганс Доббертин объявил о коллизии в алгоритме, и было предложено использовать другие алгоритмы хэширования, такие как Whirlpool, и SHA-1.
SHA-1
В 1993 году национальный Институт Стандартов и Технологии (NIST - National Institute of Standards and Technology) разработал алгоритм безопасного хеширования SHA-0. В 1995 г. он был пересмотрен и опубликован под названием FIP 180-1 (SHA-1). Позже были оперделены четыре новые версии: SHA-224, SHA-256, SHA-384 и SHA-512. Сравнерние различных версий SHA приведено в таблице:
SHA-1 является безопасным алгоритмом, поскольку в вычислительном отношении невозможно найти сообщение, которое соответствует данному дайджесу сообщения, или найти два разных сообщения, которые производят один и тот же дайджест. Любое изменение сообщения, с очень высокой вероятностью, приведет к изменению дайджеста сообщения.
Сравнение MD5 и SHA-1:
SHA-1 содержит больше шагов (80 вместо 64) и выполняется на 160-битном буфере по сравнению со 128-битным буфером MD5. Таким образом, SHA-1 должен выполняться приблизительно на 25% медленнее, чем MD5 на той же аппаратуре. Оба алгоритма просты и в описании, и в реализации, не требуют больших программ или подстановочных таблиц. Сравнение этих версий приведено в таблице:
Хэш-функции, основанные на блочных шифрах
В качестве функции сжатия можно использовать блочный шифр с симметричными ключами, например трехкратный DES или AES. Рассмотрим несколько схем для построения сжимающей функции
Сxема Рабина
Сxема Рабина базируется на схеме Меркеля-Дамгарда. Функция сжатия заменяется любым алгоритмом шифрования. Блок сообщения используется как ключ; предварительно созданный дайджест используется как исходный текст. Зашифрованный текст - новый дайджест сообщения. Размер дайджеста совпадает с размером блочного шифра данных в основной криптографической системе.
Схема Девиса-Мейера (Davies-Mayer)
В отличии от схемы Рабина использует прямую связь для защиты от атаки "сведения в середину".
Схема Матиса-Мейера-Осеаса (Metyas-Mayer-Oseas)
Это версия схемы Девиса-Мейера: блоки сообщения применяются как ключи криптосистемы. Схема может быть использована, если блоки данных и ключ шифрования имеют один и тот же размер. AES хорошо подходит для этой цели.
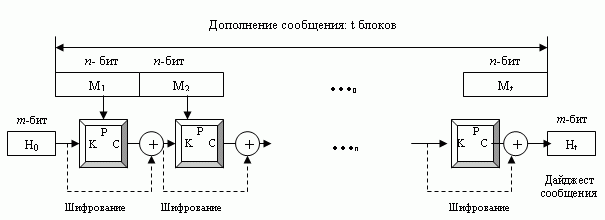
Схема Миагучи-Пренеля (Miyaguchi–Preneel)
Чтобы сделать алгоритм более устойчивым к атаке, исходный текст
, блок 
и зашифрованный текст складываются с помощью 
и создают новый блок 
. Эта схема используется в Whirlpool для создания хэш-функции.
Коллизия хэш-функций
- Коллизия хэш-функций
- Коллизией хэш-функций
называется два различных входных блока данных и 
таких, что 
.
Коллизии существуют для большинства хэш-функций, но для криптографически стойких хэш-функций частота их возникновения минимальна. Если множество различных входных данных конечно, можно задать инъективную хэш-функцию, по определению не имеющую коллизий. Однако для хэш-функций, принимающих вход переменной длины и возвращающих хеш постоянной длины (таких как MD5), коллизии обязаны существовать, поскольку хотя бы для одного значения хэш-функции соответствующее ему множество входных данных будет бесконечно — и любые два набора данных из этого множества образуют коллизию.
Мерой криптостойкости хэш-функции является вычислительная сложность нахождения коллизии. В идеале не должно существовать способа отыскания коллизий более быстрого, чем полный перебор. Если для некоторой хэш-функции находится способ получения коллизий существенно более быстрый, чем полный перебор, то эта хэш-функция перестаёт считаться криптостойкой и использоваться для передачи и хранения секретной информации.
Литература
A Critical Look at Cryptographic Hash Function
Literature
Scott Contini, Ron Steinfeld, Josef Pieprzyk, and Krystian
Matusiewicz
Centre for Advanced Computing, Algorithms and Cryptograph
y,
Department of Computing, Macquarie University
Hans Dobbertin. The Status of MD5 After a Recent Attack
RFC 3174
КатегорияКриптография