Это старая версия (1.116) КриптографическиеХэшФункции.

Криптографические xэш - функции

Хэширование

преобразование исходного информационного массива произвольной длины в битовую строку фиксированной длины.

Криптографическая хэш-функция

хэш-функция, являющаяся криптографически стойкой, то есть удовлетворяющая ряду требований, специфичных для криптографических приложений.

Требования к криптографически стойким хэш-функциям :

• Для заданного значения хэш-функции должно быть невозможно вычислить блок данных , для которого .
• Стойкость к коллизиям первого рода: для заданного сообщения должно быть вычислительно невозможно подобрать другое сообщение , для которого .
• Стойкость к коллизиям второго рода: должно быть вычислительно невозможно подобрать пару сообщений , имеющих одинаковый хэш.

Математически хэш функцию можно записать в виде: ,

где – исходное сообщение, – значение хеш-функции.

Для криптографических хэш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект).

Итеративная последовательная схема

Схема Меркеля-Дамгарда сегодня - основание для многих функций криптографического хэширования. Для построения хэш-функций используется cтруктура Меркля-Дамгарда. Cжимающая функция преобразует блоков,размер каждого состоит из бит.

В качестве начального значения переменной используется произвольное вектор инициализации . Каждый следующий блок данных объединяется с выходным значением сжимающей функции на предыдущей итерации. Если длина блока < , дополняется длиной сообщения и . Значением хэш-функции являются выходные бит последней итерации.

Функция сжатия

Односторонняя функция сжатия

функция для преобразования двух входных блоков фиксированной длины в выходной блок фиксированной длины.

В настоящее время популярны два подхода для создания хэш-функций. В первом подходе функция сжатия сделана на "пустом месте": она разработана только для этой цели. Во втором подходе блочный шифр с симметричными ключами служит функцией сжатия.

Хэш-функции, сделанные на "пустом месте"

MD5

Серия алгоритмов по построению дайджеста сообщения, была разработанна профессором Рональдом Л. Ривестом из Массачусетского технологического института. MD5 был выпущен в 1991 году для замены предыдущего алгоритма, MD4. Позже Гансом Доббертином(Hans Dobbertin) были найдены недостатки алгоритма MD4.В 1996 году Ганс Доббертин объявил о коллизии в алгоритме, и было предложено использовать другие алгоритмы хэширования, такие как Whirlpool, и SHA-1.

SHA-1

 В 1993 году  национальный Институт Стандартов и Технологии (NIST - National Institute of Standards and Technology) разработал алгоритм безопасного хеширования SHA-0. В 1995 г. он был пересмотрен и опубликован под названием FIP 180-1 (SHA-1). Позже были оперделены четыре новые версии: SHA-224, SHA-256, SHA-384 и SHA-512. Сравнерние различных версий SHA приведено в таблице:

SHA-1 является безопасным алгоритмом, поскольку в вычислительном отношении невозможно найти сообщение, которое соответствует данному дайджесу сообщения, или найти два разных сообщения, которые производят один и тот же дайджест. Любое изменение сообщения, с очень высокой вероятностью, приведет к изменению дайджеста сообщения.

Сравнение MD5 и SHA-1:

SHA-1 содержит больше шагов (80 вместо 64) и выполняется на 160-битном буфере по сравнению со 128-битным буфером MD5. Таким образом, SHA-1 должен выполняться приблизительно на 25% медленнее, чем MD5 на той же аппаратуре. Оба алгоритма просты и в описании, и в реализации, не требуют больших программ или подстановочных таблиц. Сравнение этих версий приведено в таблице:

Хэш-функции, основанные на блочных шифрах

В качестве функции сжатия можно использовать блочный шифр с симметричными ключами, например трехкратный DES или AES. Рассмотрим несколько схем для построения сжимающей функции

Сxема Рабина

Сxема Рабина базируется на схеме Меркеля-Дамгарда. Функция сжатия заменяется любым алгоритмом шифрования. Блок сообщения используется как ключ; предварительно созданный дайджест используется как исходный текст. Зашифрованный текст - новый дайджест сообщения. Размер дайджеста совпадает с размером блочного шифра данных в основной криптографической системе.

Схема Девиса-Мейера (Davies-Mayer)

В отличии от схемы Рабина использует прямую связь для защиты от атаки "сведения в середину".

Схема Матиса-Мейера-Осеаса (Metyas-Mayer-Oseas)

Это версия схемы Девиса-Мейера: блоки сообщения применяются как ключи криптосистемы. Схема может быть использована, если блоки данных и ключ шифрования имеют один и тот же размер. AES хорошо подходит для этой цели.

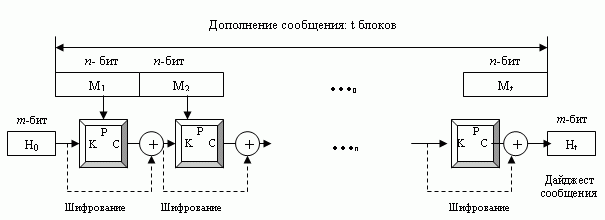
Схема Миагучи-Пренеля (Miyaguchi–Preneel)

Чтобы сделать алгоритм более устойчивым к атаке, исходный текст , блок и зашифрованный текст складываются с помощью и создают новый блок . Эта схема используется в Whirlpool для создания хэш-функции.

Коллизия хэш-функций

Коллизия хэш-функций

Коллизией хэш-функций называется два различных входных блока данных и таких, что .

Коллизии существуют для большинства хэш-функций, но для криптографически стойких хэш-функций частота их возникновения минимальна. Если множество различных входных данных конечно, можно задать инъективную хэш-функцию, по определению не имеющую коллизий. Однако для хэш-функций, принимающих вход переменной длины и возвращающих хеш постоянной длины (таких как MD5), коллизии обязаны существовать, поскольку хотя бы для одного значения хэш-функции соответствующее ему множество входных данных будет бесконечно — и любые два набора данных из этого множества образуют коллизию.

Мерой криптостойкости хэш-функции является вычислительная сложность нахождения коллизии. В идеале не должно существовать способа отыскания коллизий более быстрого, чем полный перебор. Если для некоторой хэш-функции находится способ получения коллизий существенно более быстрый, чем полный перебор, то эта хэш-функция перестаёт считаться криптостойкой и использоваться для передачи и хранения секретной информации. Литература

 %R(

 %A Scott Contini 
 %A Ron Steinfeld
 %A Josef Pieprzyk 
 %A Krystian Matusiewicz
 %T A Critical Look at Cryptographic Hash Function Literature
 %I     New Jersey, USA : World Scientific Publishing
 %P 22
 %D 2008
 %U http://events.iaik.tugraz.at/HashWorkshop07/papers/Pieprzyk_CriticalLook.pdf
 

 %A Norman Matloff
 %T The Art of R Programming
 %D 2009

 %A Lipin B. R.
 %A Sitkarev G. A.
 %B AM&P Lab reports
 %T The Beginner's Guide to Art of Bad Code and Ugly Style
 %D 2015
 %R)

Centre for Advanced Computing, Algorithms and Cryptograph y, Department of Computing, Macquarie University Hans Dobbertin. The Status of MD5 After a Recent Attack RFC 3174

---

КатегорияКриптография